天华中威科技微波小课堂_什么是MIMO?MIMO基本技术原理

天华中威科技微波小课堂_什么是MIMO?MIMO基本技术原理
什么是MIMO

多进多出（multiple input multiple output，MIMO）是为极大地提高信道容量，在发送端和接收端都使用多根天线，在收发之间构成多个信道的天线系统。

多进多出是一种相当复杂的天线分集技术。多径效应会影响信号质量，因此传统的天线系统都在如何消除多径效应上动脑筋。而MIMO系统正好相反，它利用多径效应来改善通信质量。在MIMO系统中，收发双方使用多副可以同时工作的天线进行通信。MIMO系统通常采用复杂的信号处理技术来显著增强可靠性、传输范围和吞吐量。发射机采用这些技术同时发送多路射频信号，接收机再从这些信号中将数据恢复出来。
MIMO基本技术原理

随着无线通信技术的演进，为了提高信息的传输速率和带宽利用率，多天线技术应用而生，即MIMO，从香农公式的角度来看，MIMO技术之所以能够提高数据传输速率，本质上是提高信噪比。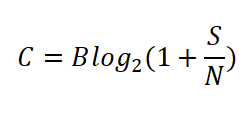

广义理解的MIMO，指的是同时支持多层传输数据流传输的这样一种空分复用方式。但是有时候，比如我们说5G中的massive MIMO，指的是波束管理beamforming技术。MIMO技术最基本的原理。我们可以围绕以下三点进行理解：

• 1、为什么可以用多个天线分别独立传输不同的数据流呢？
  

• 2、此时如何保证它们互不不干扰？
  

• 3、为什么在接收端可以恢复出来？
  

为了更容易理解MIMO的基本原理，我们首先看下mimo的数学模型：

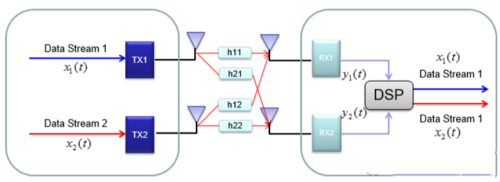
图片来源：ShareTechnote

我们假设此时两个数据流同时到达，比如说两个TB，分别由两个天线单独发送，两路发送数据经过无线信道系统，到达两个接收天线，收端通过数字信号处理，把两个流的数据分别独立恢复出来。需要注意的是：在发送端，两路信号的RF端调制的时候采用的是同一个频率段，比如5G 100M情况下,那两路信号都是采用100M带宽。仅仅是增加了天线数。

Note:这个模型的实现要求收发天线数需要大于等于流数。

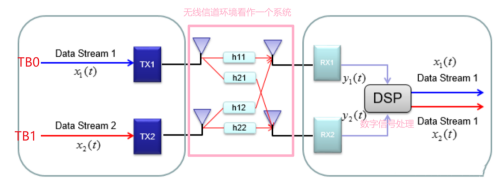
对于多数据互不干扰的原因，我们可以先假设有这样一种情况：两路信号在空间传输的时候经历的是两条不相关的信道或者说是完全正交的信道，所以传输的时候也是完全正交的，能够做到互不干扰。

从数学模型的角度可以这样解释：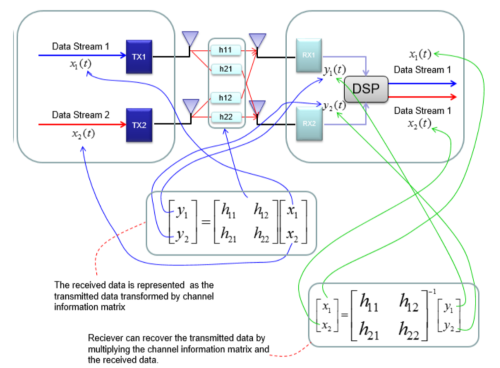

其中Y是我们收到的两路数据，H是信道矩阵，即信道参数的集合。X是我们发送的两路数据流。我们的目的：由收到的Y1/Y2通过计算得到两路互不干扰的X1/X2。 

由上图可以看出来，计算出X的直接方法是求H的逆，此时发送数据=信道H的逆*接收数据。

那么，这里的信道矩阵H是如何得到呢？

信道矩阵H首先应该采用参考信号估计出来，参考信号其实就是一些训练序列，是先验已知的信号，无论是4G/5G我们都需要用这样的参考信号去估信道。我们还是根据如下公式先将H计算出来：

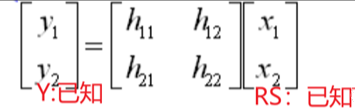
此时不仅Y是已知的，X也是已知的训练序列（参考信号）。

当收端把H求出来以后，通常我们的接收机有两种做法：

1、收端立即把H反馈给发端，发端据此对发送数据进行预处理（预编码）；（闭环）

2、收端不反馈H,直接计算相应时频资源内发送的未知数据信号X；(开环)

关于参考信号RS的说明：

由于移动通的信道条件随时间/距离改变而变化。从时间轴来看，比如由某个子帧，某个时隙的某个参考信号计算出的H，与该时隙附近的其他参考信号计算出来的H并无太大变化。但时间继续拉长，可能大有不同，此时就不能重复使用前面的H。所以我们在系统设计的时候需要考虑参考信号的密度。密度越大，H较准，误码率较低。但是密度太大也会占用我们的频带资源，比如5g就优化了参考信号的设计，不再使用CRS，从而提高数据传输速率。

H矩阵的秩Rank，实现双流传输的条件 

根据mimo的数学信道模型，我们可以得出以下二元一次方程组：

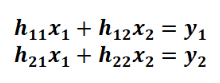
此时想要解出,则必须要求：

举个例子：2*x_1+3*x_2=y_1

                 4*x_1+6*x_2=y_2

此时无法解出x_1/2，因为系数矩阵是线性相关的。此时信道矩阵的秩=1，但是假设矩阵元素依次2/3/4/5则可以解析出来，此时矩阵的秩=2。其实秩的大小就是能独立传输的数据流数。

为了能够解析出发送数据，面临的问题是：

1. 需要获得一个不相关的信道矩阵；

2. 需要求出信道H的逆，但实际情况是并不是所有的矩阵的逆都存在；

3. 矩阵求逆是一个复杂的过程。

因此，我们需要对发送数据进行预处理，使得收端在解码的时候无需求信道H的逆便可解析出X。

方法：SVD,将H分解为三个矩阵，如下图所示:

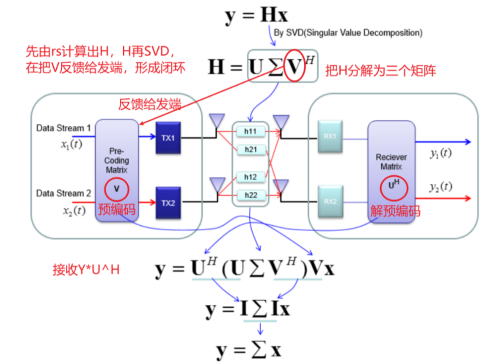
而是一个对角矩阵，因此，如下图所示，这就可以简单的求出发送数据了。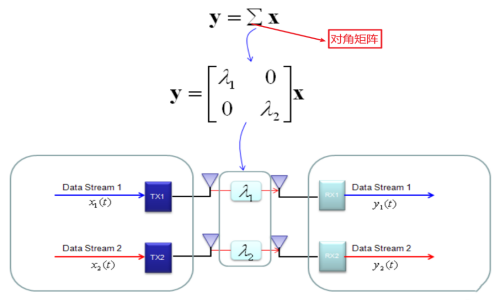

以上就是天华中威科技小编为您整理的课堂的所有内容，感谢您的来方访。