隐形杂散射频工程师也可以用EVM来排查

EVM是什么？

在星座图中，会有一个理想的点，然后还有一个实测的点。

就是一个是打算在哪，另一个是实际在哪。

再换句话说，就是一个是理想，一个是现实。

星座图中的点，其与原点连接的矢量，所对应的长度和角度，分别对应信号的幅度和相位。

理想点与原点的连接，是一个参考的矢量。

实测点与原点的连接，是一个实测的矢量。

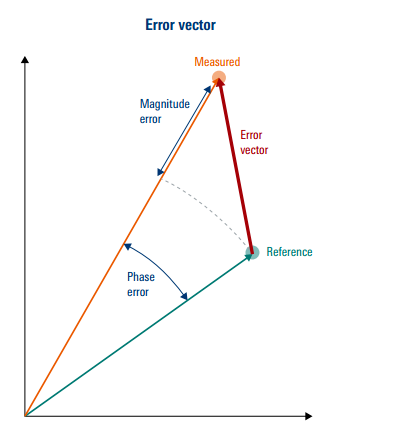
而理想点与原点的连接，就被称为误差矢量(error vector)。

和所有矢量一样，误差矢量有幅度，有方向。

在数字调制中，主要关注误差矢量的幅度，不纠结方向。

因此，最重要的测量目标，是误差矢量的幅度，即EVM，全称为error vector magnitude.

人都知道，理想与现实的差距越小越好。

所以，误差矢量的幅度，也是越小越好。

那差别主要来自哪里呢？

一个来自幅度误差(magnitude error)，也就是说接收到的矢量与参考的矢量相比，要么太长，要么太短。

一个来自相位误差(phase error),也就是说接收到的矢量与参考的矢量相比，角度有差。

EVM大，则代表测量点和理想点之间的距离很大。

也就是说理想点A所对应的测量点，可能与理想点B的位置更接近。

这样，会导致接收端误判的概率提高。

因此，减小EVM，是无线通信系统中的重要目标之一。

对EVM造成影响的因素主要有哪些？

影响EVM的因素，可以分为四大类，分别为幅度影响，相位影响，I/Q不平衡，配置因素。

说到幅度影响。

首先，与幅度相关的因素，都可能会影响EVM。

比如说，信号太高，导致器件进入非线性；或者信号太低，容易受噪声影响，此时都会增加EVM。

比如说，外界干扰，或者系统内的杂散，也会影响EVM。

比如说，相应带宽内不平坦的频率响应，也可能增加EVM。

.......

说到相位影响。

也就是说，与相位相关的因素，都会可能影响EVM。

比如说，信号相噪的影响。我的理解是这样的(欢迎批判)：本身相位调制是基于理想相位的，如果相位噪声太高的话，理想相位本身就不理想了。

比如说，相位响应随频率的变化而变化。我的理解是这样的(欢迎批判)：可以理解为群时延随着频率的变化有抖动，这样的话，不同频率的信号经过时，其相位变化也会不一样，导致EVM增加。

还有就是I/Q不平衡。

比如说增益不平衡，相位不平衡，直流馈通等。

说到配置因素。

就包括发端和收端，设置的匹配滤波器的类型或参数，符号率等设置的有差别。

EVM计算时的注意点

EVM计算时，会归一化。

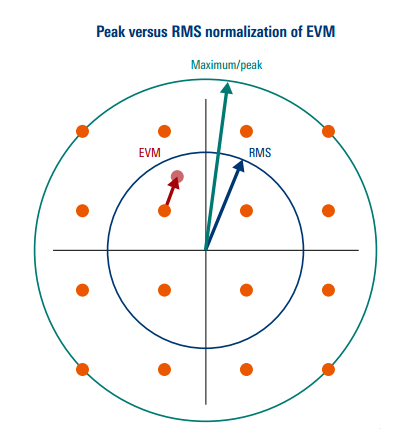
有两种归一化的方法，一种是用最大峰值功率来归一化；另一种，是用RMS功率来归一化。

在比较EVM时，需要保证使用同样的归一化方法。

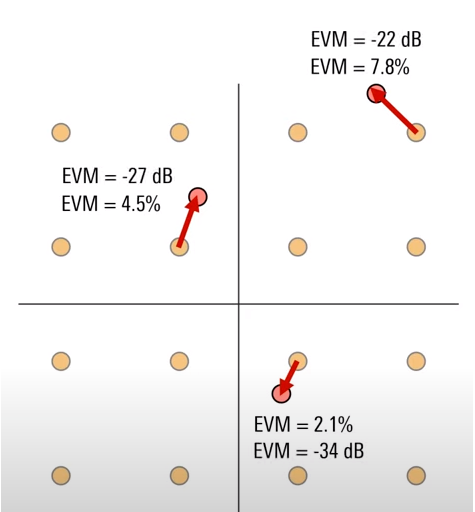
EVM的单位可以是%，也可以是dB。

对于单位为%的EVM值，小的百分比值，表示更好的EVM。

对于单位为dB的EVM值，通常为负值，越负，EVM越好。

EVM在debug中的作用

重点来了哈！虽然说，我没有用过这种方法来进行过debug。

但是看上去，好像很好用的样子。

首先，看看EVM随时间变化的曲线的作用。

EVM是基于每个符号进行计算的，也就是说，每个符号都会计算EVM。

因此，EVM可以绘制成时间的函数，也可以看成连续符号的函数。

比如如下图，发送和接收符号率之间细微的差异，使得EVM随时间变化的曲线呈现出一个V形曲线。

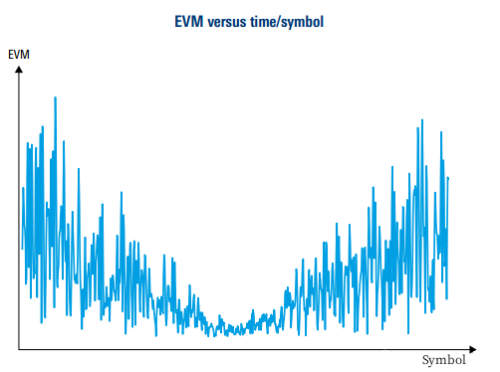
突发或者脉冲信号，在开始或结束的时候，由于各种放大器效应或时序的影响，EVM可能会高点。

如果幅度随时间变化，可能会使得幅度相对较高或者幅度相对较低的符号的EVM变大。

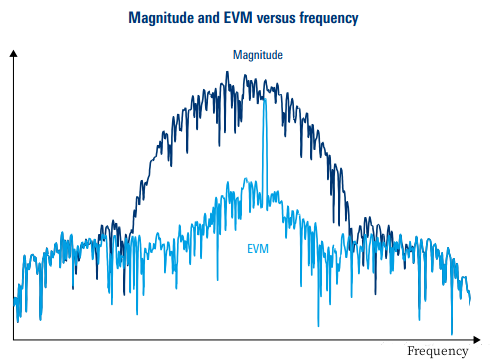
EVM也可以绘制成随频率的曲线。

EVM随频率变化的函数，是对上面的EVM随时间变化的函数进行FFT变换。

而这个曲线最有用的应用，是可以发现带内的杂散信号或者干扰。

如下图所示，蓝色曲线为幅度谱，看不出任何有杂散信号。青色曲线为EVM谱，上面可以明显的看到带内杂散性。

这是因为，叠加有杂散信号的有用信号的EVM，只会在杂散频率处变高。

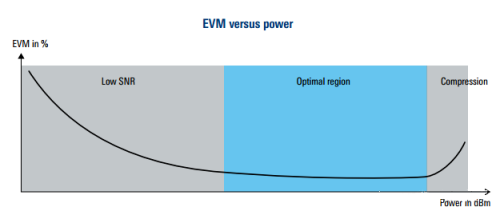
还有EVM与功率之间的关系，即看EVM随着输入功率变化的函数。

如下图所示，曲线为一个浴缸形状的曲线。低输入电平时，SNR较小，导致较高的EVM；高输入电平时，器件进入非线性，EVM也会恶化。

所以，这个EVM与功率的曲线，可以用来确定器件的最优工作区域。

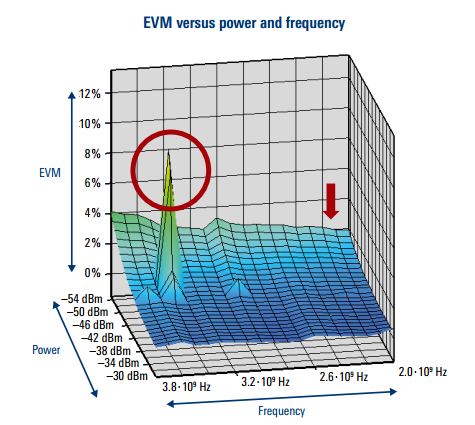
EVM随功率以及频率变化的曲线

在三维空间内，绘制EVM随功率和频率变化的曲线，可以很容易的找出被测器件的随频率变化趋势或者问题区域。

参考文献:

[1] Rohde&Schwarz White Paper，UNDERSTANDING EVM