[技术前沿]一种面向密集道路汽车雷达场景的相互干扰抑制算法

调频连续波（FMCW）毫米波雷达可在全天候条件下工作，从而在汽车行业得到广泛采用。由于道路上毫米波雷达的密度增加，安装在自车辆上的主雷达面临相互干扰的问题。 

传统的检测方案一般采用一维快速傅里叶变换（FFT），然后对中频（IF）信号采用恒虚警报率（CFAR）来获得目标检测。但是，在相互干扰的情况下，中频信号的行为异常，传统的信号处理框架容易导致漏检和误检。 

论文《A Mutual Interference Mitigation Algorithm for Dense On-Road Automotive Radars Scenario》提出了一种针对中频 (IF) 信号的加权拍频信号归一化算法，然后采用传统的检测方案作为相互干扰缓解机制。

论文链接：https://ieeexplore.ieee.org/document/10234787

加权拍频信号归一化算法的实现很简单，因为不会干扰架构中的任何处理模块，例如混频器、LPF、FFT 和 CFAR 模块。仿真结果表明，所提方法提高了信干噪比（SINR），从而降低了漏检目标的概率。

注：在FMCW雷达中，中频（IF Signal）、差频、拍频（beat signal）、差拍本质上都是指同一个概念。

一、概述

调频连续波 (FMCW) 雷达工作在不同的频率范围，即 24 GHz、60 GHz、77 GHz 和 80 GHz，以便实现远程雷达 (LRR) 和短程雷达 (SRR) 应用 [1] 。 这些雷达传感器采用单芯片构建，输入功率低，可在雾、雪、雨和无光条件下工作，提供如跟踪 [2]、环境感知 [3]、成像 [4]、分类 [5]、舱内健康监测系统 [6]、纳米和微米物体检测 [ 7]和场景成像[8]各种功能。 

汽车行业正在通过提供毫米波雷达和其他汽车传感器（摄像头、激光雷达、超声波等）以及多传感器融合，将现有的L1、L2升级到L4系统[9]。随着道路交通中毫米波雷达密度的增加，雷达会产生无意干扰的问题。汽车行业正在研究各种方法来检测干扰，然后减轻干扰，以及从损坏的信号中恢复信号[10]。

脉冲幅度控制、噪声消除器和参差脉冲重复频率 (PRF) 等信号处理技术用于减少干扰影响 [11]、[12]。脉冲压缩等传统方法也应用于 FMCW 传感器数据以减轻干扰 [13]。此外，OFDM-MIMO（正交频分复用-多输入多输出）和认知雷达技术用于执行可调Q因子小波变换并抑制干扰 [14]。 

文献[15]提出了一种修剪精确线性时间已知变化数（PELT-KCN）算法，通过利用峰值变化和加权包络归一化（WEN）来抑制 FMCW 雷达干扰。 此外，研究界尝试将短时傅里叶变换（STFT）技术与拍频插值[16]和一维恒虚警率（CFAR）归零[17]相结合来减轻干扰。同时，该问题也通过 OS-CFAR 和基于全局最近邻扩展卡尔曼滤波器（GNN-EKF）的目标跟踪得到解决[18]。 

最初，这种干扰缓解问题仅限于信号处理和目标跟踪，后来扩展到机器学习（ML）和深度学习（DL）技术的新兴领域，全连接卷积神经网络和量化卷积神经网络（CNN）也是雷达干扰缓解的潜在候选者[19]、[20]。

从文献[11]-[13]来看，这些传统技术对于脉冲雷达来说已经得到了很好的发展，并且对于当前的毫米波LFM波雷达也具有适用性。需要注意的是，参差PRF和脉冲幅度控制技术需要重新设计波形合成器。ML 和 DL 技术非常适合研究， 同时，数据收集和数据大小对于开发基于干扰抑制的 ML 和 DL 算法至关重要 [19]、[20]。 

在不改变现有硬件或数据收集的情况下，最优的解决方案应该非常轻便可行。这促使我们提出了一种加权拍频信号归一化算法，用于减轻时域中的相互干扰，从而通过 FFT 和 CFAR 获得检测结果。这种方法不会中断 CFAR 检测或跟踪框架的实际过程，该算法可作为 IF 信号和 FFT 模块之间的附加模块。

本文的结构如下，第二节介绍数学模型和建议的方法。随后，第三节和第四节分别给出了模拟结果和结论。

二、相互干扰缓解

本节推导了相互干扰的数学模型， 然后提出加权拍频信号归一化算法。

2.1 数学模型

汽车雷达通常采用FMCW雷达，考虑如图 1（a） 所示的密集道路交通模型，其中主雷达位于自我车辆上，其他辅助雷达位于交通参与者上，这里的交通参与者是指其他道路车辆。

主雷达面临着视场（FOV）内二次雷达的相互干扰，反之亦然。毫米波雷达的主要职责是探测视场内的目标，以执行自动巡航控制、紧急制动辅助、路径跟踪等功能。

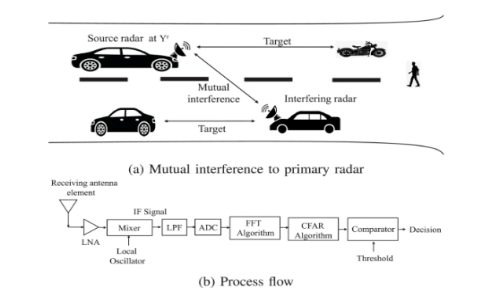
图1：场景图解及传统检测算法步骤

1）无干扰环境

主雷达发射持续时间为 Tc、斜率为 S、载波频率为 fc 的快频波信号。发射信号 s(t) 的数学表示为：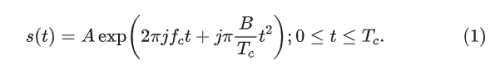 

这里，A 是传输信号的振幅，B 是带宽。斜率 S 的计算公式为：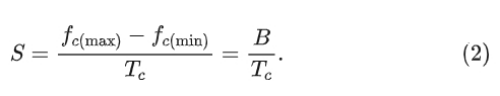  

作为雷达算法工程师，公式和信号模型需要熟记于心，都是很简单的。fc(max) 和 fc(min) 是 fc 的最大和最小频率。根据公式（1），指数信号的第一部分包含 fc。而公式（1）中指数信号的第二部分提供了传输信号的频率，其值为：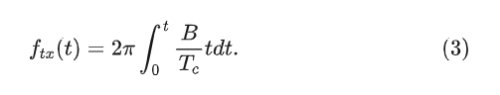 

信号 s(t) 碰到目标，反射回来的信号为 r(t)。FOV范围内N个目标的接收信号模型为 ：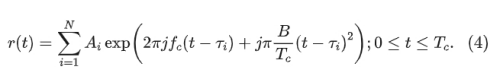

这里，Ai 是接收到的振幅，τi 是目标 i 的往返时间延迟。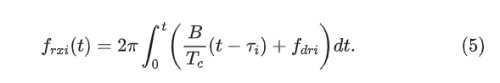  

同时，目标i对应的往返行程为：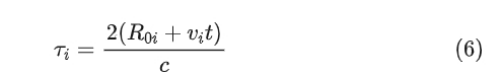  

R0i 是目标 i 的起始范围，c 是自由空间中的速度，vi 是第 i 个移动目标的速度。同样，fdri 是目标 i 的多普勒频移，计算公式为：  

其中，λ 表示波长。如图 1（b） 所示，接收信号 r(t) 送入混频器，然后进行低通滤波（LPF）。高频被去除，下变频后的信号为：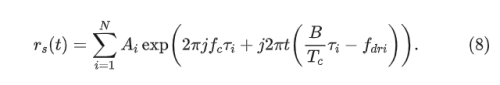 

在上述下变频后的IF信号上，应用快速傅立叶变换（FFT）和恒虚警率（CFAR）检测方案来检测目标。为了简化和更好地理解，假设FOV 内没有任何相互干扰的两个目标，并遵循图 1(b)所示的流程。因此，拍频频率可视化如图 2（a）所示。相应地，目标检测结果可视化如图 2(b) 所示。 

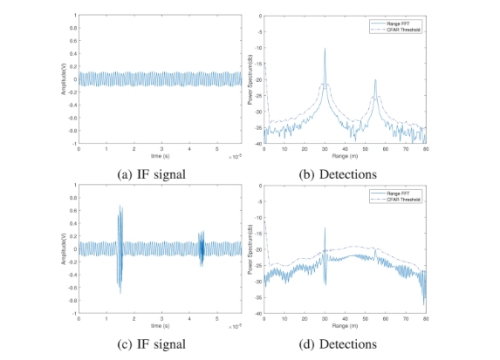
图2：(a) 无干扰的节拍信号 (b) 无干扰环境下的检测 (c) 有干扰的节拍信号和 (d) 干扰环境下的检测

2）干扰环境

在这种情况下，主雷达的总接收信号有两个原因。第一个信号是主雷达从 N 个目标发射-反射回来的信号，如公式(8)所示。第二个信号来自 M 个二次雷达发射和一次雷达接收，如图 1(a) 所示。

在此模型中，假定所有毫米波雷达都是同一类型：相同的频率、带宽和Chirp持续时间。接收信号的模型为：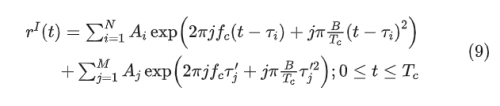

整个接收到的信号经过混频器和 LPF 后得到 IF 信号，即：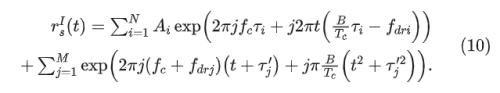  

与无干扰情况类似，IF 信号通过 FFT 和 CFAR 块来获得目标检测结果。为简化问题，考虑两个目标（N = 2）和两个干扰源（M = 2）。

有干扰的情况下的IF 信号如图 2(c) 所示，相应的检测结果如图 2(d) 所示，可以看出，由于雷达相互干扰，目标存在漏检。 

2.2 加权拍频信号归一化算法

加权拍频信号归一化算法可以识别IF信号的变化，并通过将IF信号包络与阈值进行比较来进一步最小化幅度。 其中，阈值是通过使用前向和后向样本计算，IF包络通过阈值进行归一化。 

因此，通过消除干扰信号来提高信号干扰比（SINR)，该算法的伪代码通过将IF 信号作为输入来减轻干扰，流程如下所示:

输入：IF信号  

输出：加权拍频信号归一化IF信号

步骤1：前向滑窗，通过长度为 l 的前向滑动窗口估计最大包络。

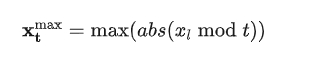
步骤2：前后滑窗，通过长度为 l 的前后滑动窗口估计最大包络。

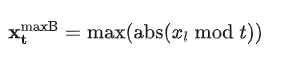
步骤3：估计最小值，选择前向或后向包络的最小值。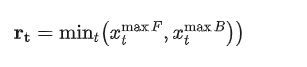

步骤4：估计权重，IF 信号通过每个滑动窗口中的权重 wt 进行归一化。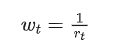

2.3 加权拍频信号归一化算法处理流程

加权拍频信号归一化算法可以消除干扰效应,并减少误检的数量，加权拍频信号归一化算法可以作为一个额外的处理块来实现，从而不用修改现有的硬件。

加权拍频信号归一化算法消除干扰效果的方法是在时域IF信号中进行的，通过使用前后向加窗技术可以消除IF信号内的毛刺， 该过程适用于每一个Chirp信号，不需要任何先验信息。图3给出了在存在干扰的情况下检测目标的改进流程。

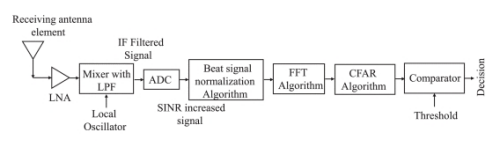
图3：加权拍频信号归一化算法处理流程

三、仿真结果

3.1 仿真场景

设置毫米波雷达参数为：

（1）工作频率为 77GHz、线性调频脉冲持续时间为 59μs、带宽为 99MHz、采样频率为 5MHz。

（2）目标1和目标2分别在 30 m 和 55 m 处，同时雷达的最大范围为80m，干扰引入到同频率的毫米波雷达中。

由于干扰，出现了如图2（c）所示的被破坏的IF信号，同时，在IF上应用 STFT 的时频图如图 4 所示。图 4(a)显示了无干扰 IF 信号上的 STFT，而图 4(b)显示了受干扰IF 信号上的 STFT。 

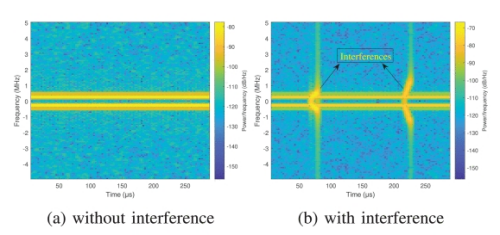
图4：IF 信号的STFT

3.2目标检测

如图3所示，加权拍频信号归一化算法块用于处理IF信号。在该算法中，窗口是可调参数，它以滑动方式向前和向后移动。在处理后的IF 信号上应用一维 FFT，然后应用CA-CFAR检测技术，其中有1个保护单元和6个参考单元。

在无干扰情况下，在30 m和55 m处检测到两个目标，如图2(b)所示。

在干扰的情况下，传统的检测算法（见图1(b)）会导致漏检（见图2(d)）。

为了检测淹没在干扰中的目标，论文使用了所提出的算法流程（参见图 3）。图5(a)和图5(c)分别描绘了窗口大小为80和200的加权和归一化拍频信号。

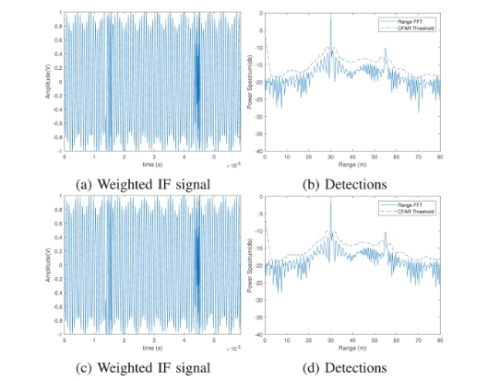
图5：IF信号（a 和 c）和检测（b 和 d）窗口长度分别为 80 和 200 。

同样，可以通过采用所提出的流程从图 5（b） 和图 5(d) 中观察到成功的检测。表 I 中提供了所有情况的 SNR。还观察到，与图 2(d) 相比，功率谱有所增加，这是 CA-CFAR 检测（30 m 和 55 m）的主要原因 。

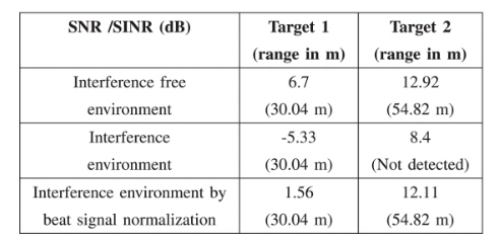
表1： SNR变化

3.3 窗长大小的影响

本算法唯一可调的参数是窗长大小，窗长对目标检测的影响如表2所示。

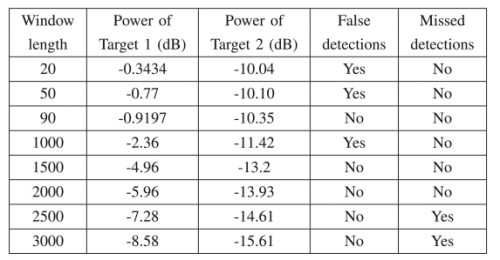
表2：窗长对目标检测的影响

实验观察到较小窗长（20 和 50）存在错误检测。窗长（90）的进一步增加既不会导致错误检测，也不会导致漏检。此外，窗长的增加（超过 2500）会导致漏检。 

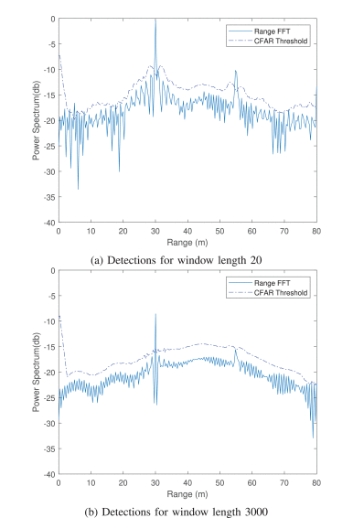
图6：显示了窗口长度为20的目标检测

图6（a）显示了窗口长度为20的目标检测，在5m、30m和55m处观察目标。其中， 5m处的检测为误报，这种误报背后的原因是由于窗长较小，与 CFAR 阈值相比噪声功率增加。 

此外，图 6(b) 给出了 30m处的一个目标检测，即使场景中存在两个目标。由于两个目标都落在相同的窗长内，因此会出现这种漏检。通过权重归一化后，功率会降低，导致CFAR算法漏检。因此，必须选择合适的窗长，以便获得真实的目标信息。

四、总结

道路中毫米波雷达密度的增加导致雷达间干扰，传统的接收机架构（由混频器、LPF、FFT和CFAR组成）无法减轻相互干扰，导致目标漏检。 

本文提出的加权拍频信号归一化算法来处理IF信号，通过该算法，IF信号的突然波动以前后向滑动窗口的方式被归一化。

加权拍频信号归一化算法很容易实现，因为它不会干扰任何现有的接收器架构处理模块。仿真结果表明，选择较小的窗长会导致错误目标增加。此外，较大的窗长会导致漏检。通过适当的窗长可以检测到干扰范围内的淹没目标，并且不会出现误报或漏检。

这个算法研究的未来方向可以集中于窗长大小的最优选择或基于IF信号历史的自适应窗长。此外，还可以通过裁剪干扰信号并通过寻找自适应权重对其进行处理来进一步修改算法。

扩展阅读：

1、FMCW汽车雷达干扰及干扰缓解算法仿真(含MATLAB代码)

2、雷达著作翻译 | 《现代雷达在汽车中的应用》第4章干扰和干扰缓解（4.1 | 4.1.2.1小节）

3、城市“电子战”（City EW） | 汽车雷达传感器的反干扰技术