天华中威科技微波小课堂_ADC模拟到数字转换器介绍

ADC是模拟到数字转换器（Analog-to-Digital Converter）的缩写。它是一种电子设备或模块，用于将连续变化的模拟信号转换为离散的数字信号，以便数字系统（如微处理器、微控制器等）能够对其进行处理和分析。

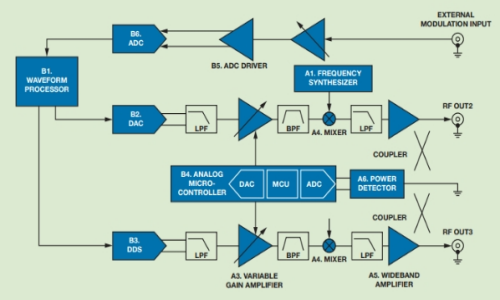
将模拟信号转换成数字信号的电路，称为模数转换器（简称A/D转换器或ADC，Analog to Digital Converter），A/D转换的作用是将时间连续、幅值也连续的模拟信号转换为时间离散、幅值也离散的数字信号，因此，A/D转换一般要经过采样、保持、量化及编码4个过程。

ADC建立了模拟世界的传感器和数字世界的信号处理与数据转换的联系。当然，数字信号通过处理器处理后，也可以通过DAC还原回去。

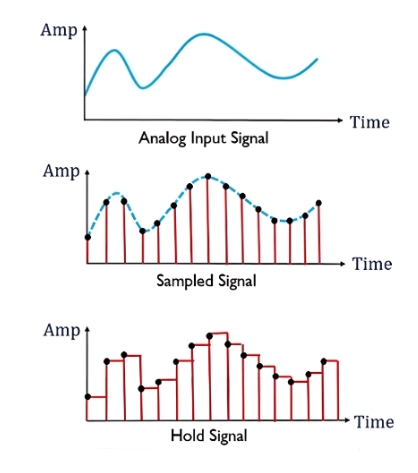
采样

采样是将时间上连续变化的信号，转换为时间上离散的信号，即将时间上连续变化的模拟量转换为一系列等间隔的脉冲，脉冲的幅度取决于输入模拟量。这里采样需遵循奈奎斯特采样定理，即当采样频率大于模拟信号中最高频率成分的两倍时，采样值才能不失真的反映原来的模拟信号。FS≧2F

保持

模拟信号经采样后，得到一系列样值脉冲。采样脉冲宽度一般是很短暂的，在下一个采样脉冲到来之前，应暂时保持所取得的样值脉冲幅度，以便进行转换。因此，在采样电路之后须加保持电路。

输入的模拟信号电压经过采样保持后，得到的是阶梯波。

采样 - 保持电路的基本形式如下：    

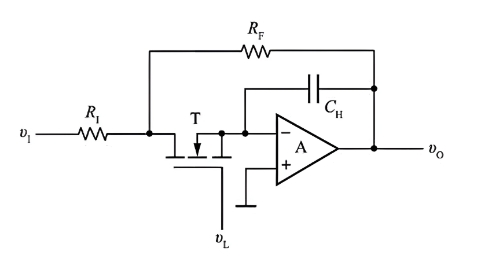
采样 - 保持的基本步骤：

当采样控制信号 vL 为高电平时，使 MOS 管 T 导通，v1 经过电阻 1 和 MOS 管 T，给电容 CH 充电。

若取 R1=RF，则充电结束后 v0=vc=−v1。

当采样控制信号 vL 为低电平，MOS 管 T 截止，电容 CH 上的电压不会突变，所以 v0 也能保持一段时间，采样结果得以被记录下来。

量化

采样得到的数字量，必须为某个规定的最小数值单位的整数倍，这个转换过程称为量化，所取的最小数量单位称为量化单位 Δ。数字信号最低有效位 LSB（last significant bit） 的 1 所代表的数量大小就等于 Δ。    

LSB=Vref/2N

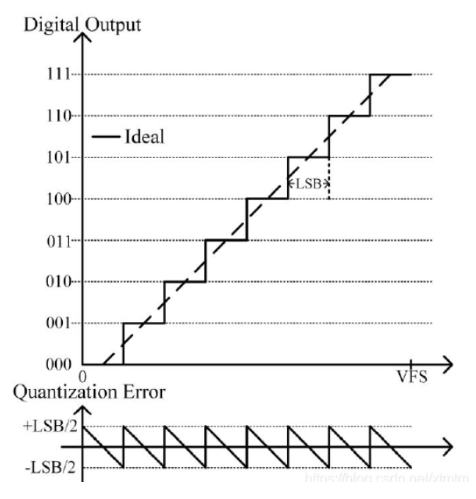
因为模拟电压是连续的，不一定能被 Δ 整除，因此会出现量化误差。

量化级越细，量化误差就越小，所用二进制代码的位数就越多，电路也越复杂。    

编码

将量化的结果用二进制(或其他进制)表示出来，称为编码。

ADC的指标参数  

一、基本参数  

分辨率  

ADC分辨率为用于表示模拟输入信号的位数。为了更准确地复现模拟信号，就必须提高分辨率。使用较高分辨率的ADC也降低量化误差。对于DAC，分辨率与此类似：DAC的分辨率越高，增大编码时在模拟输出端产生的步进越小。

采集时间    

采集时间是从释放保持状态(由采样-保持输入电路执行)到采样电容电压稳定至新输入值的1 LSB范围之内所需要的时间。采集时间(Tacq)的公式如下：

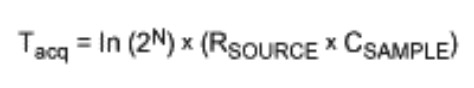
式中，RSOURCE为源阻抗，CSAMPLE为采样电容，N为分辨率位数。

建立时间  

对于DAC，建立时间是从更新(改变)其输出值的命令到输出达到最终值(在规定百分比之内)之间的时间间隔。建立时间受输出放大器的摆率和放大器振铃及信号过冲总量的影响。对于ADC，采样电容电压稳定至1 LSB所需的时间小于转换器的捕获时间至关重要。

最低有效位(LSB)  

  最低有效位又称最小分辨率，满量程值除以ADC的分辨率就是LSB。在二进制数中，LSB为最低加权位。通常，LSB为最右侧的位。对于ADC，LSB的权重等于转换器的满幅电压范围除以2N，其中N为转换器的分辨率。对于12位ADC，如果满幅电压为2.5V，则1LSB = (2.5V/212) = 610µV

量程（full-scale range, FSR）   

对ADC芯片，量程指芯片允许输入模拟信号范围，与dBm有一定对应关系，单位一般用dBFS。在满量程之前，dBFS与dBm呈线性关系，即XdBm减小1dB，则XdBFS对应减小1dBFS。    

dBFS是数字信号电平单位，简称满度相对电平。Full Scale 指0 dBFS 的位置, 0 dBFS就是最大编码电平，不同ADC的0 dBFS 实际对应值不同，它也是数字峰值表满度的参考电平。数字信号以ADC能处理的最大模拟信号的编码为最大值，即0 dBFS, 实际数字信号的幅度的编码相对于这个最大值的信号编码所代表的幅度之比，即为满度相对电平（dBFS）。因为规定最大值为0 的位置，所以，一片ADC实际处理的信号的满度相对电平都是负值。                         

二、静态参数  

微分非线性(DNL)误差  

对于ADC，触发任意两个连续输出编码的模拟输入电平之差应为1 LSB (DNL = 0)，实际电平差相对于1 LSB的偏差被定义为DNL。对于DAC，DNL误差为连续DAC编码的理想与实测输出响应之差。理想DAC响应的模拟输出值应严格相差一个编码(LSB)(DNL = 0)。

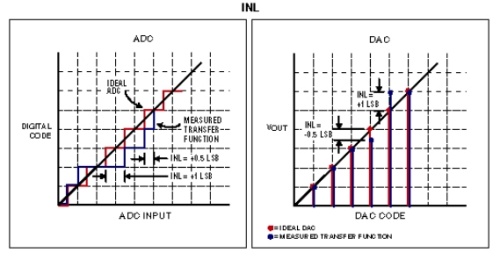
积分非线性(INL)误差  

对于数据转换器，积分非线性(INL)是实际传递函数与传递函数直线的偏差。消除失调误差和增益误差后，该直线为最佳拟合直线或传递函数端点之间的直线。INL往往被称为“相对精度”。    

三、动态参数  

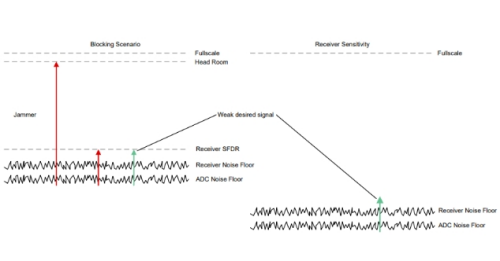
动态范围  

动态范围定义为器件本底噪声至其规定最大输出电平之间的范围，通常以dB表示。ADC的动态范围为ADC能够分辨的信号幅值范围；如果ADC的动态范围为60dB，则其可分辨的信号幅值为x至1000x。对于通信应用，信号强度变化范围非常大，动态范围非常重要。如果信号太大，则会造成ADC输入过量程；如果信号太小，则会被淹没在转换器的量化噪声中。

互调失真(IMD)  

IMD是指由于电路或器件的非线性产生的原始信号中并不存在的新频率分量的现象。IMD包括谐波失真和双音失真。测量时，将其作为将所选交调产物(即IM2至IM5)的总功率与两个输入信号(f1和f2)的总功率之比。2阶至5阶交调产物如下：

2阶交调产物(IM2)：f1 + f2、f2 - f1

3阶交调产物(IM3)：2 x f1 - f2、2 x f2 - f1、2 x f1 + f2、2 x f2 + f1

4阶交调产物(IM4)：3 x f1 - f2、3 x f2 - f1、3 x f1 + f2、3 x f2 + f1

5阶交调产物(IM5)：3 x f1 - 2 x f2、3 x f2 - 2 x f1、3 x f1 + 2 x f2、3 x f2 + 2 x f1

信噪比(SNR)  

信噪比(SNR)是给定时间点有用信号幅度与噪声幅度之比，该值越大越好。对于由数字采样完美重构的波形，理论上的最大SNR为满幅模拟输入(RMS值)与RMS量化误差(剩余误差)之比。理想情况下，理论上的最小ADC噪声仅包含量化误差，并直接由ADC的分辨率(N位)确定：

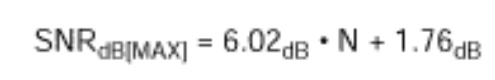
(除量化噪声外，实际ADC也产生热噪声、基准噪声、时钟抖动等。)

总谐波失真(THD)  

实际器件的转换过程中电路的非线性会引入谐波失真信纳比（SINAD）表示信号与噪声和谐波失真总能量的比值SINAD=SNR+THD

THD测量信号的失真成分，用相对于基波的分贝(dB)表示。测量时，只有在奈奎斯特限值之内的谐波被包含在内。

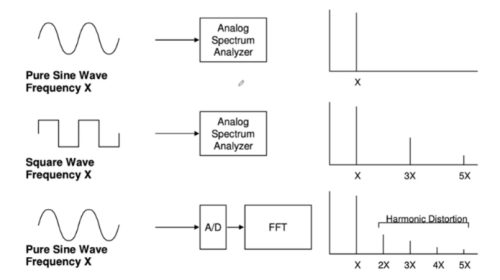
信纳比(SINAD)  

SINAD是正弦波(ADC的输入，或DAC恢复的输出)的RMS值与转换器噪声加失真(无正弦波)的RMS值之比。RMS噪声加失真包括奈奎斯特频率以下除基波和直流失调以外的所有频谱成分。SINAD通常表示为dB。

有效位数(ENOB)    

ENOB表示一个ADC在特定输入频率和采样率下的动态性能。理想ADC的误差仅包含量化噪声。当输入频率升高时，总体噪声(尤其是失真分量)也增大，因此降低ENOB和SINAD(参见“信号与噪声+失真比(SINAD)”)。满幅、正弦输入波形的ENOB由下式计算：

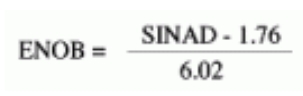
过采样  

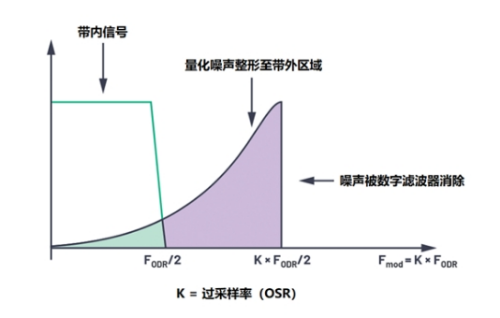
对于ADC，如果采样模拟输入的频率远远高于奈奎斯特频率，则称为过采样。过采样有效降低了噪底，所以提高ADC的动态范围。提高动态范围又进而提高了分辨率。过采样是Σ-Δ ADC的基础。

对于理想ADC而言，SQNR代表信噪比SNR。对于奈奎斯特速率的ADC，可通过增加采样位数，改善SNQR。对于Sigma-Delta ADC，通过K倍过采样，将量化噪声扩展至KFs/2，降低Fs/2内的噪声功率，同样改善了SNQR。

6.02N+1.76dB+10Log（K/2）